If you’ve ever seen a compound bow in action, the first thing you probably noticed was the blistering speed of its arrows. After that, though, you may have wondered at its seemingly complex and mechanically intricate design. With its many cables, wheels and strangely shaped pulleys, it looks more like part of a sailing rig than a bow.
However, all these mechanical intricacies are exactly what produce that incredible arrow speed, not to mention the destructive force when it hits its target. How they do that may seem a bit complex at first, but it’s actually a very elegant application of mathematics and classical mechanics, specifically the pulley system.
By understanding how a compound bow works, you can gain a full appreciation of the machine and more readily take advantage of its resulting power. With a full overview of a compound bow’s anatomy and how these parts utilize physics, you will come to see why compound bows have become so popular in the archery world since their invention in 1966.
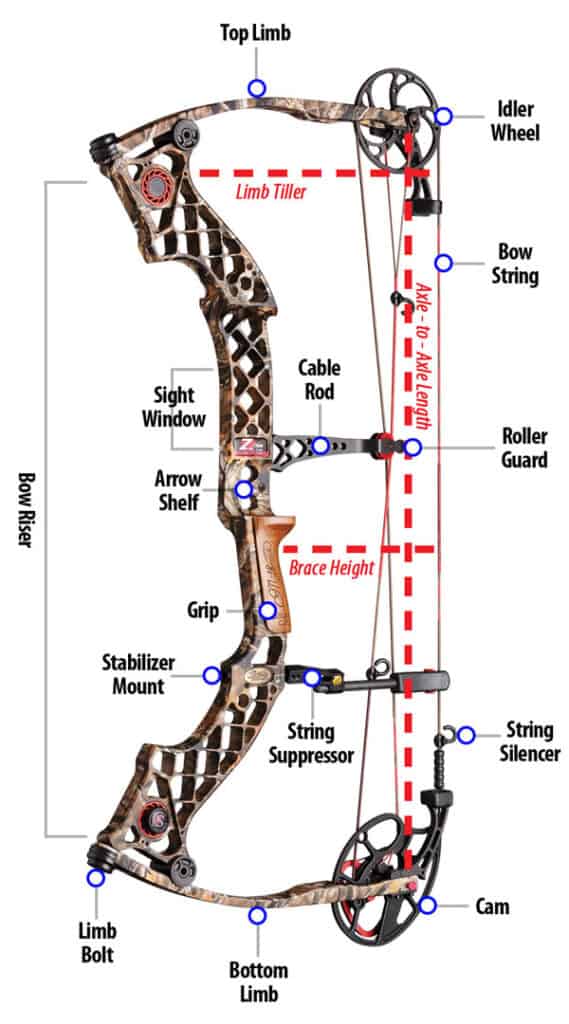
Anatomy of a Bow
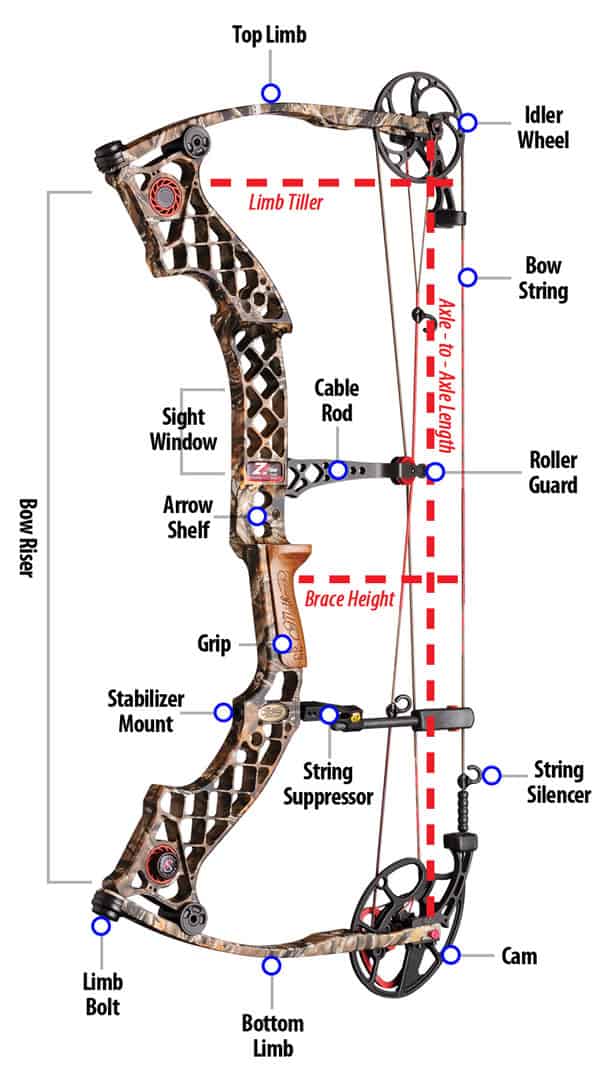
Credit to Bowhunting.com
To understand compound bows, you first have to understand the basic foundation they’re built on. All bows, compound and otherwise, have a fundamental basic design. First, some kind of flexible material forms a stave. In the old days, this was made of wood, but modern bows may be a combination of wood, metal and synthetic material. Regardless, the stave is the main part of the bow and forms some variation on a D shape.
The stave is divided into the limbs and risers. The center piece is called the riser, while the thin, bendy arms that stretch up and down from the riser are called the limbs. While ancient bows were often a single piece of wood, it’s easy to tell the riser from the limbs on modern bows, especially compound bows, because they’re usually separate manufactured pieces that have been bolted together.
Along with a stave, a complete bow is formed by attaching a bowstring to the end of each limb. Bowstrings are also made of tough, flexible material, but despite popular belief, you don’t really stretch the bowstring when you pull it back. Rather, the bowstring bends the limbs. This action takes advantage of the laws of physics to launch an arrow at high speeds despite not having any outside energy source besides what you can produce with your own body.
Basic Bow Physics
The most amazing thing about a bow is that it can shoot an arrow at speeds of hundreds of miles per hour, but this speed is entirely produced by energy from your own muscles. There’s no electricity, no explosive gunpowder, just pure elbow grease. But of course, you can’t throw an arrow at hundreds of miles an hour. Most people couldn’t throw an arrow at hundreds of feet an hour. So what is it about bows that use the body’s own power so much more efficiently?
One of the most important principles in physics is that energy is always conserved. For example, when you push a cart up a hill, all that energy you used pushing it up there is conserved as potential energy in the cart, even if it’s sitting at the top of the hill not moving. Give it a tap, and it’ll roll back down the hill, all that potential energy turning back into kinetic energy, or movement.
Basically, bows work like big, weirdly shaped springs, which are great devices for storing potential energy. When you pull back the bowstring, it bends the limbs of the bow, storing most of the energy your arm and back muscles produce in the limbs themselves. If you hold the bowstring drawn back, this energy remains stored in the limbs. However, if you let go of the bowstring, the limbs snap back and release all that stored energy. They pull the bowstring with them, and if there’s an arrow attached to it, launch it out of the bow.
To understand why this results in such high speeds, take a look at the basic formula for kinetic energy:
Here, m refers to the mass of the object and v its velocity. As you can see, these two things are multiplied together to get the kinetic energy. Well, dust off your algebra and think about the relationship if we have a constant amount of E, kinetic energy. The smaller the mass, the higher the velocity necessary to equal the same amount of energy. Arrows, of course, are extremely lightweight. As a result, all that energy you stored in the limbs gets turned mostly into velocity.
Draw Weight and Draw Length
These physics principles have a lot of implications for bow operation. First, consider that the more energy you can put into the bow, the faster and farther you can shoot the arrow. Since your body is the only source of energy for the bow, this means more work for your muscles.
For a traditional bow, the harder it is to pull the bowstring back, the more energy you’re storing in the limbs. This is rated in something called draw weight and is measured in pounds just like weight due to gravity. In other words, drawing a bow weighted at 75 pounds of draw weight takes as much effort as lifting a 75-pound weight off the floor.
This is complicated a bit by draw length, or the distance from the bowstring’s rest point to full draw. This is because the farther you pull back the bowstring, the more difficult it becomes. This means that the farther back you draw the bow, the more energy you can store in the limbs and transfer to the arrow. Plus, a longer draw length gives the bow more time to accelerate the arrow before it leaves the bow, thereby transferring energy into it.
While these physical principles produce amazing results, they do have limits. For example, even the biggest strongman in the world has a maximum draw weight he could handle. Even the tallest man in the world has a maximum draw length his arms could utilize.
To get more power, energy, and speed out of our bows, we can’t just up the numbers. Instead, we have to employ even more physics principles to create a more advanced tool. This is the compound bow.
Special Compound Bow Anatomy—Cams
The compound bow differs from its traditional cousins, the longbow and recurve bow, primarily due to its use of cams. The most basic compound bows have one cam system located at the end of one of the limbs, complemented by a simple timing wheel on the other limb. More modern, complex compound bows may feature cam systems on each limb. Regardless, compound bows, just like their ancient predecessors, only use energy produced by your body, just in a more complex and ingenious way.
Cam systems feature one small wheel attached to a larger wheel by the same axle. When you draw the bowstring, it pulls on these wheels and rotates the larger wheel. The larger wheel in turn rotates the smaller wheel. Due to the principles of physics and pulley systems, which we will discuss shortly, this produces something called let-off.
Let-off
The advantage of a compound bow is that it lets you pull back the same amount of draw weight as a conventional bow with a lot less effort, specifically a lot less force. For example, imagine a compound bow with a 60-pound draw weight and 75% let-off. This means that the limbs will store the same energy it would take you to lift 60 pounds off the ground—or draw a conventional 60-pound bow for that matter—but you won’t have to apply 60 pounds of force. Rather, you’ll have to apply 75% less force, only 15 pounds.
For most compound bows, the let-off isn’t linear, though. This is because the cams are usually shaped somewhat like eggs in an eccentric pulley system. As a result, drawing the bow gets harder and harder, then levels out towards the middle, before getting easier and easier until it reaches a point where it suddenly gets incredibly, usually impossibly, difficult again. This is called the valley and is the point of full draw for a compound bow.
To understand the let-off and valley, take a look at this graph:
As you can see, the draw weight increases before decreasing again during the let-off. Compare this to the linear and steady increase for a conventional recurve bow.
A Review of Pulley Systems
Cams may look a bit complicated, and it may not be immediately clear why they lower the draw weight so dramatically. The answer lies in the physics of a simple machine called a pulley. Humans have understood and taken advantage of pulleys for thousands of years. The ancient Egyptians even utilized them to move the enormous stones with which they built the pyramids, even if they hadn’t worked out the mathematics of exactly why they worked yet. The most fundamental physics principle at play in the pulley system is the relationship between work, force and energy.
Work
Firstly, work can be defined as the transfer or change of kinetic energy. When we’re talking about kinetic energy, this is basically just one object moving another. When you push a car, you’re doing work by transferring energy from your muscles and body to the car. Similarly, when you draw a bowstring, you’re doing work by transferring energy from your muscles into the bow limbs, which then transfer it into the arrow as we know from basic bow physics.
So now let’s take a look at the formula for work:
This, like pretty much all our physics formulas in classical mechanics, comes from Newton’s second law of motion in which Force is equal to mass times acceleration. Additionally, the distance the object travels has a direct relationship with its velocity which has a direct relationship with its acceleration. Specifically, the distance formula looks like this:
Here v stands for velocity and a for acceleration. Plug ma (mass times acceleration) in for F in the work formula and the above formula in for d. Multiply out the terms, and you get this:
That should look familiar. Each term in that formula is simply the equation for kinetic energy, so work then is just the final kinetic energy minus the initial kinetic energy, or the change in kinetic energy.
Force and Distance
Now that we’ve shown that Force multiplied by distance, i.e. work, is indeed the same as the change or transfer of kinetic energy, we can think about the relationship between force and distance. Basically, if we want to do a certain amount of work and thereby transfer a certain amount of energy, adjusting force or distance will adjust the other as well.
Thinking algebraically, something may stand out to you. We can decrease the amount of force required to perform a certain amount of work by increasing the amount of distance over which we do it. Let’s say we want to do 10 foot-pounds of work. As the unit of measurement implies, this is the amount of work required to lift a 10 pound weight one foot. Well now let’s say we lift a five-pound weight two feet. The amount of work and therefore energy is the same, but it took much less force to do it because there is less mass.
Pulley systems take advantage of this principle. If you have to get a 10-pound weight a foot off the floor, how can you do the same amount of work but decrease the required force? In other words, how can you increase the distance over which you apply the force? Thread a rope through a pulley system above you, and you have your answer.
With one pulley, the distance over which you apply the force doubles. That’s because for every foot you lift the weight, you have to pull the pulley two feet, one foot between the pulley and weight, and one foot between the pulley and you. By doubling the distance, you halve the force. Add another pulley, such as in a block and tackle system, and you halve it again.
Cams as Pulleys
All this mathematical manipulation may seem like magic, but it has serious results. Any regular compound bow archer will tell you that it doesn’t take any more force to draw their compound bow than a traditional archer to draw their recurve. Many times it even takes less force and is easier to hold at full draw. Nevertheless, compound bow speeds approach nearly double that of their conventional counterparts.
But how exactly do cams act like pulleys? They’re obviously round like pulleys, but they seem a bit more complex than your basic flagpole pulley. Cams are an even more advanced pulley system adapted perfectly for archery. This involves a system of cables and multiple wheels and pulleys.
Inner and Outer Wheels
The cam system’s most ingenious aspect is the use of inner and outer wheels on the pulley system. The bowstring itself is attached to the outer wheel, so when you draw it, that’s where the force is applied. However, a smaller wheel is attached to the same axle, so it turns as well.
Now think back to our work formula and the relationship between force and distance. When you draw the bowstring, it’s transferring most of that energy into the pulley system. It’s doing a certain amount of work. By turning its smaller partner, the big wheel is transferring part of that energy then to the smaller wheel through work too.
But wait. The smaller wheel can’t move as far as the big wheel. We have to think about some trigonometry and geometry to prove this. Specifically, the circumference of a circle is equal to its diameter times 𝜋.
Let’s say the big wheel is 8 inches in diameter. This means its circumference is 8𝜋. Now imagine it turns 90 degrees, or a quarter of the way around. Well just divide our circumference by 4 and you see it’s traveled exactly 2𝜋 inches.
Now think about the smaller wheel, which we’ll say has a diameter of 4 inches for a circumference of 4𝜋. It will also turn 90 degrees, or a quarter of the way around, so divide its circumference by 4 as well. This shows you that the smaller wheel has only traveled 𝜋 inches, half the distance of its big brother.
Well, we already know more distance means less force, but now we have it the other way around. The smaller wheel travels less distance which means it will apply more force to its cable than the bowstring applied to the bigger wheel. The cables attached to the smaller wheel or wheels then pull the limbs together with considerable force, storing considerable energy.
As an extra bonus, the perpendicular positioning of the cables with regards to the limbs provides extra leverage and allows them to store more energy than a conventional bow in which the bow string must pull the limbs at an angle. All of these mechanical advantages together turn the compound bow into the incredible feat of science, physics and technology that it is.
What Is the Result?
If you’ve made it through all that physics jargon, you may finally be wondering, OK, I get how compound bows work, but what good does that do me? Are they really that much better than conventional bows?
Better is subjective, of course, and many archers prefer traditional bows like recurves and longbows for a number of reasons. However, there’s no debating that compound bows are faster, more powerful, and more deadly than conventional vertical bows. While traditional bows occasionally reach arrow speeds of 200 FPS (feet per second), there are compound bows on the market that hit over 350 FPS.
For one thing, faster arrows mean more accuracy. That’s because for a certain amount of distance traveled, they don’t have as much time to drop or be affected by outside factors like wind. Plus, as we know from our physics, high velocity arrows mean lots of kinetic energy. If you’re a hunter, it’s this energy that translates to killing power. As it’s transferred into your target, that work transforms into destructive force.
Closing Words

It’s no wonder then that these bows are popular with bowhunters and target archers alike. Manufacturers invent new models and improve upon these basic physics principles each year. Now that you have a general understanding of its mechanics, you too can enjoy the technological marvel that is the modern compound bow.